明魔法零知识证上隐私保学遇当数护的
作者:0xAlpha DeriProtocol联合创始人 | 编译:DODO Research团队
zk-SNARK的奇妙世界
想象一下,你能向别人证明自己知道某个秘密,却不用透露秘密本身的内容——这就是zk-SNARK(零知识简洁非交互式知识论证)的魅力所在。作为一个经常和密码学打交道的从业者,我至今仍为这项技术的精妙设计感到惊叹。
让我用一个日常生活中的类比来解释:就好比你向酒店前台证明自己确实预订了房间,但完全不需要出示身份证件或预订确认码。听起来像魔术?这正是数学带给我们的现实魔法。
从问题到证明的四步舞曲
构建zk-SNARK证明就像是在跳一支精心编排的舞蹈,需要经历四个关键步骤:
1. 首先,我们要把问题转化为算术电路——这就像把一道复杂的数学题拆解成基础的加减乘除运算。
2. 接着,将这些运算关系用矩阵公式来表示。
3. 然后,神奇的事情发生了——我们把这些矩阵公式转化为多项式,并找到它们之间的整除关系。
4. 最后,在椭圆曲线的加密空间里完成整个证明过程。
前三步其实都是在做"翻译"工作,把问题用不同的数学语言重新表述。真正精彩的是第四步,利用同态加密技术把证明过程搬到加密空间里进行,就像在镜中世界完成魔术表演,既证明了事实,又保护了秘密。
数学基础:你需要知道这些
理解这篇文章只需要大学一年级的代数知识。唯一可能让人犯怵的是椭圆曲线加密,但其实把它想象成一个具有特殊性质的指数函数就行——关键在于它的逆向计算至今仍是个数学难题。
在正式讲解前,我们先约定一些符号规则:矩阵用粗体大写字母(如A),向量用小写字母加箭头,标量就是普通字母。记住这些,待会看公式就不会晕头转向了。
实战案例:爱丽丝的证明之旅
让我们通过一个具体例子来理解整个过程。假设爱丽丝想证明她知道函数f(x)=x³+x²+5的一个解。虽然这个例子很简单,但它能清晰展示zk-SNARK的核心原理。
有趣的是,即便遇到包含if-else的复杂函数,我们也能轻松转化为类似的算术表达式。比如:
f(x,z) = (z-1)(x²+5) + z(x³+x²+5)
这个技巧让我想起编程中的条件表达式,只不过现在我们用纯数学的方式来表达逻辑分支。
第一步:构建算术电路
我们把f(x)分解成最基本的运算步骤:- s1 = x × x- s2 = s1 × x- s3 = s1 + s2- y = s3 + 5
这就像把一道复杂菜肴的烹饪过程拆解成切菜、炒制、调味等基础动作。每个步骤都形成一个"约束条件",总共4个约束构成了我们的算术电路。
第二步:矩阵的魔法
接下来,我们定义一个见证向量s = [1, x, s1, s2, s3, y],然后构造三个矩阵A、B、C。通过矩阵乘法,我们就能用s·A·s·B = s·C来表示所有约束条件。
这个过程最考验耐心的是逐行构建矩阵,确保每个算术门都能正确对应。就像拼乐高积木,必须确保每个零件都卡在正确的位置。
第三步:多项式的艺术
现在,我们要把这些矩阵转化为多项式。这就像是把离散的数据点连成平滑的曲线。使用拉格朗日插值法,我们可以找到满足条件的多项式PA、PB、PC。
最终我们会得到形如P(z) = t(z)h(z)的等式,其中t(z)是预设的多项式,h(z)是商多项式。这个可整除关系是整个证明的关键所在。
第四步:椭圆曲线上的加密之舞
最精彩的部分来了!我们要在椭圆曲线上完成证明。椭圆曲线密码学就像是在一个特殊的数字宇宙里进行运算,这里的基本单位是曲线上的点。
理解椭圆曲线点加法有个形象的比喻:想象在桌布上画一条曲线,用直尺找到两点间的交点,然后像折纸一样把这个点对称翻转到曲线另一侧,这就是"加法"的结果。
我们还需要引入双线性映射这个神奇工具,它允许我们在加密空间中进行乘法运算。这就像是在戴着手套的情况下完成精细的拼图操作。
完整的证明流程
在实际操作中,我们需要先生成公共参考字符串(称为验证钥VK)。有趣的是,无论问题多复杂,VK始终只需要7个椭圆曲线点。这让我想起万能钥匙的概念——同样的锁具可以保护无数个不同的保险箱。
爱丽丝生成证明的过程本质上是进行了一系列椭圆曲线点的线性组合。而验证过程则像在进行三重安全检查:
1. 确认证明中的点确实是参考点的合法组合
2. 验证各项系数的正确性
3. 检查最终的等式是否成立
为什么这很重要?
作为一个见证了区块链技术发展的从业者,我深刻体会到zk-SNARK的革命性意义。它让我们能在不泄露隐私的前提下完成验证,这在金融、医疗、投票等领域都有巨大应用潜力。
回想第一次理解这个机制时的震撼,就像突然看懂了魔术师的秘密手法。数学的深邃之美,往往就藏在这些看似简单的等式背后。
推荐阅读
Vitalik Buterin的《Zk-SNARKs: Under the Hood》
Thomas Chen等人的《零知识证明综述》
Maksym Petkus的《zk-SNARK工作原理权威解释》
零知识证明相关维基百科条目
相关文章
 今天我想跟大家分享一个真实的故事,这可能是近两年加密圈最励志的逆袭案例之一。主人公予与,一个普通的90后,用8年时间完成了从5万本金到上亿资产的惊人跨越。但这个故事里没有神话,只有普通人死磕到底的执着。机缘巧合的入场2017年,还在大学校园里的予与因为一个摄影群里的偶然讨论,第一次听说了莱特币。那时候比特币才几千美元,整个加密市场还处于早期野蛮生长阶段。和大多数人一样,他最初也只是玩现货买卖,结果...2025-09-16
今天我想跟大家分享一个真实的故事,这可能是近两年加密圈最励志的逆袭案例之一。主人公予与,一个普通的90后,用8年时间完成了从5万本金到上亿资产的惊人跨越。但这个故事里没有神话,只有普通人死磕到底的执着。机缘巧合的入场2017年,还在大学校园里的予与因为一个摄影群里的偶然讨论,第一次听说了莱特币。那时候比特币才几千美元,整个加密市场还处于早期野蛮生长阶段。和大多数人一样,他最初也只是玩现货买卖,结果...2025-09-16 这两天盯着盘面看,真心觉得市场情绪开始出现微妙变化。大饼(BTC)的走势特别有意思,每次回调的低点都比前一次要高那么一点点,像极了爬楼梯的节奏。而以太坊(ETH)昨晚的表演简直惊心动魄,直接从悬崖边上一头栽向1903美元,看得人手心冒汗。不过市场总是充满戏剧性,就在大家以为要跌破心理防线的时候,以太坊在1903这个神奇的位置突然来了个华丽转身,一鼓作气冲到了1970附近。这种强势反弹可不是闹着玩的...2025-09-16
这两天盯着盘面看,真心觉得市场情绪开始出现微妙变化。大饼(BTC)的走势特别有意思,每次回调的低点都比前一次要高那么一点点,像极了爬楼梯的节奏。而以太坊(ETH)昨晚的表演简直惊心动魄,直接从悬崖边上一头栽向1903美元,看得人手心冒汗。不过市场总是充满戏剧性,就在大家以为要跌破心理防线的时候,以太坊在1903这个神奇的位置突然来了个华丽转身,一鼓作气冲到了1970附近。这种强势反弹可不是闹着玩的...2025-09-16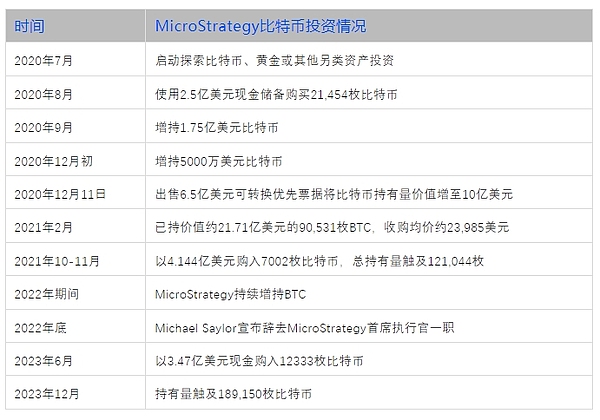 最近在研究DeFi的时候,我突然意识到一个有趣的问题:在这个新兴的加密世界里,会不会诞生下一代的贝莱德或先锋基金?要知道,截至2022年,全球资产管理规模高达126万亿美元,相当于全球金融财富的38.3%。而加密资产管理规模才区区几百亿美金,占比不到3%,这差距简直像蚂蚁和大象的对比。信任是资管行业的命脉资管行业说白了就是"代客理财"。你把钱交给专业人士打理,他们帮你投资股票、债券、房地产等各种资...2025-09-16
最近在研究DeFi的时候,我突然意识到一个有趣的问题:在这个新兴的加密世界里,会不会诞生下一代的贝莱德或先锋基金?要知道,截至2022年,全球资产管理规模高达126万亿美元,相当于全球金融财富的38.3%。而加密资产管理规模才区区几百亿美金,占比不到3%,这差距简直像蚂蚁和大象的对比。信任是资管行业的命脉资管行业说白了就是"代客理财"。你把钱交给专业人士打理,他们帮你投资股票、债券、房地产等各种资...2025-09-16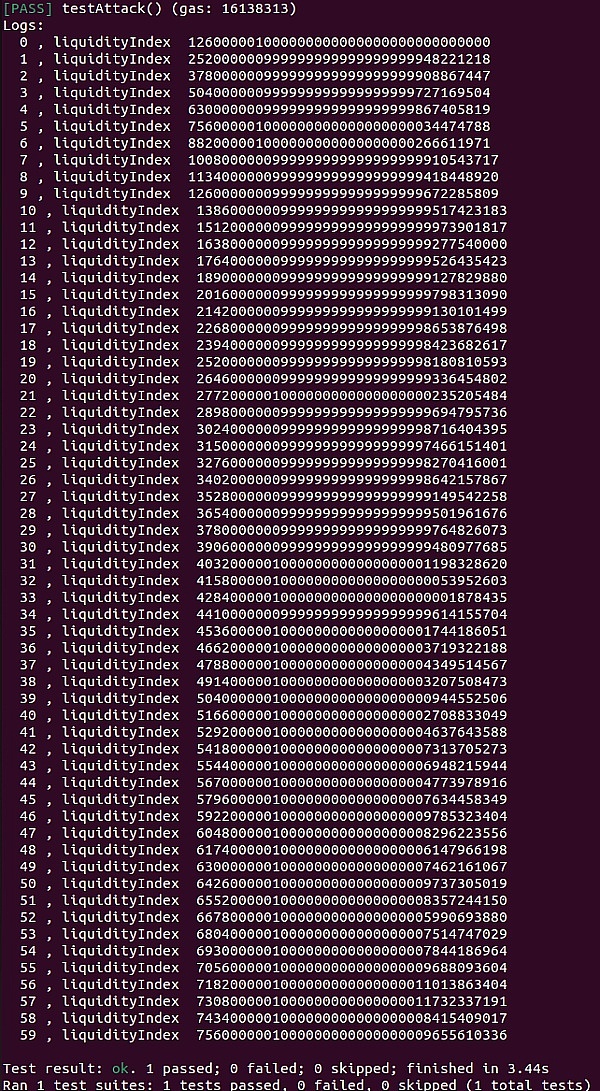 说实话,做交易就像在走人生的路,处处都是选择题。记得上周我还在跟朋友抱怨,看着账户里的盈利数字跳动时,那种纠结啊——到底该不该落袋为安?而当行情反转时,又想掐死那个犹豫不决的自己。以太坊市场实战复盘就拿11月16号的行情来说吧,那天早上我盯着盘面看了好久。以太坊的回调让我想起了小时候玩的那种跳跳板,跌下去总会弹起来。2035美元附近那个位置,我几乎是咬着牙补仓的——现在看来这决定真是明智。结果你们...2025-09-16
说实话,做交易就像在走人生的路,处处都是选择题。记得上周我还在跟朋友抱怨,看着账户里的盈利数字跳动时,那种纠结啊——到底该不该落袋为安?而当行情反转时,又想掐死那个犹豫不决的自己。以太坊市场实战复盘就拿11月16号的行情来说吧,那天早上我盯着盘面看了好久。以太坊的回调让我想起了小时候玩的那种跳跳板,跌下去总会弹起来。2035美元附近那个位置,我几乎是咬着牙补仓的——现在看来这决定真是明智。结果你们...2025-09-16 今早的市场真是给我开了个大大的玩笑!本来周末都准备好喝咖啡看行情平稳波动了,谁知道大饼(BTC)突然一个猛冲直奔27000美元,以太(ETH)也不甘示弱地突破1650美元。这种"周末突袭"的戏码在币圈虽然不罕见,但每次都能让不少人措手不及。说实话,这种急涨行情最让人纠结。看着价格蹭蹭往上涨,内心那个追高的冲动简直按捺不住。但老韭菜的经验告诉我:这种时候往往就是陷阱。昨晚以太回踩1610的时候,圈子...2025-09-16
今早的市场真是给我开了个大大的玩笑!本来周末都准备好喝咖啡看行情平稳波动了,谁知道大饼(BTC)突然一个猛冲直奔27000美元,以太(ETH)也不甘示弱地突破1650美元。这种"周末突袭"的戏码在币圈虽然不罕见,但每次都能让不少人措手不及。说实话,这种急涨行情最让人纠结。看着价格蹭蹭往上涨,内心那个追高的冲动简直按捺不住。但老韭菜的经验告诉我:这种时候往往就是陷阱。昨晚以太回踩1610的时候,圈子...2025-09-16 作为一名在加密圈摸爬滚打多年的观察者,我得说Starknet这次在代币设计上的创新确实让人眼前一亮。记得去年Solana的黑客事件吗?无数用户的资产就因为一个简单的授权漏洞而付之东流。而现在,Starknet的STRK代币似乎要为这个行业痛点带来治愈方案。账户控制权的历史性转变传统ERC-20代币最让人头疼的就是那个Approve功能。我们经常能看到这样的场景:用户随手点个授权,就把自己钱包的生杀...2025-09-16
作为一名在加密圈摸爬滚打多年的观察者,我得说Starknet这次在代币设计上的创新确实让人眼前一亮。记得去年Solana的黑客事件吗?无数用户的资产就因为一个简单的授权漏洞而付之东流。而现在,Starknet的STRK代币似乎要为这个行业痛点带来治愈方案。账户控制权的历史性转变传统ERC-20代币最让人头疼的就是那个Approve功能。我们经常能看到这样的场景:用户随手点个授权,就把自己钱包的生杀...2025-09-16

最新评论